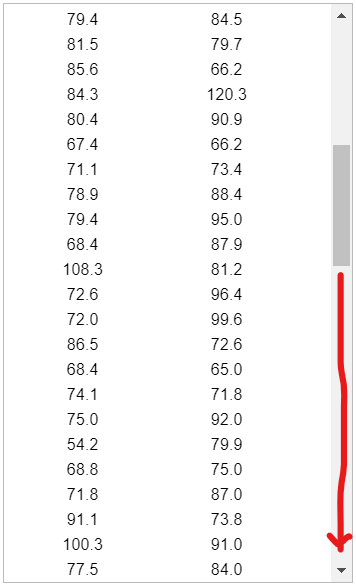
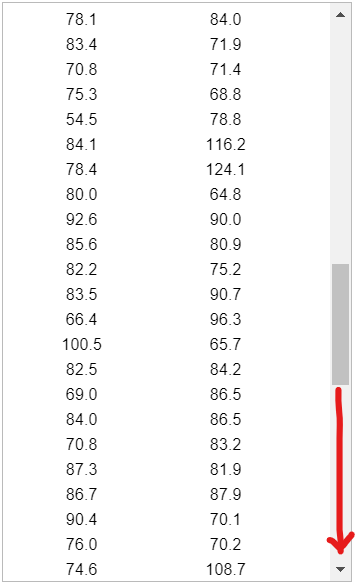
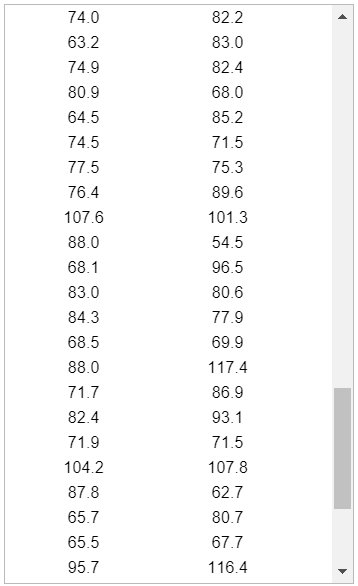
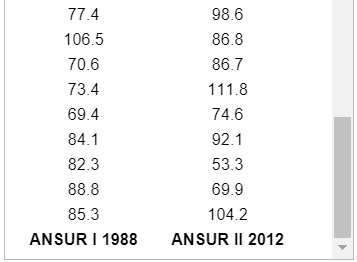
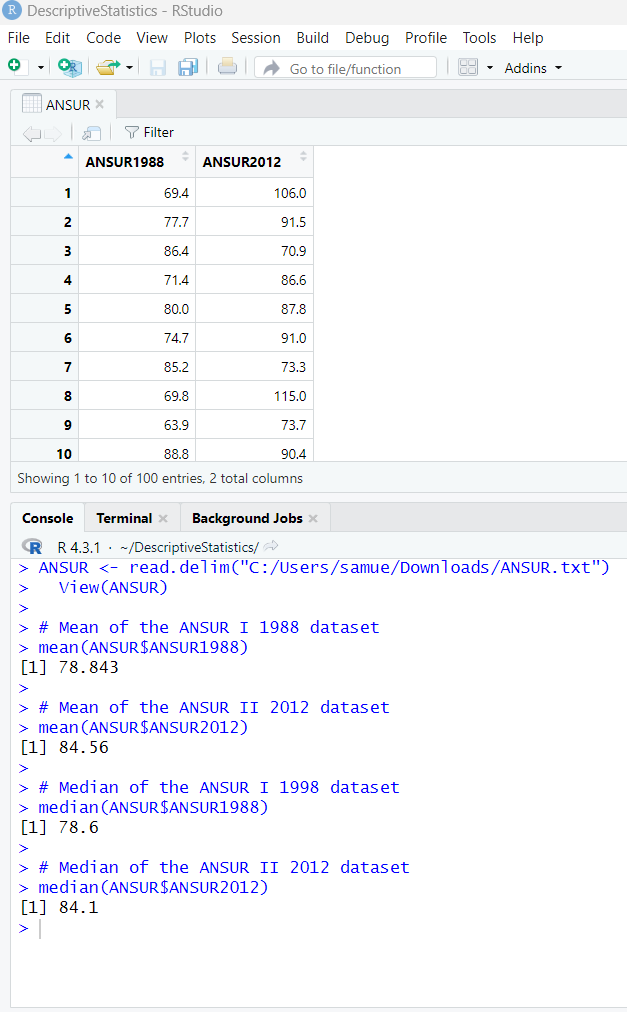
(3.) Use the magnitudes (Richter scale) of the earthquakes listed in the data set below.
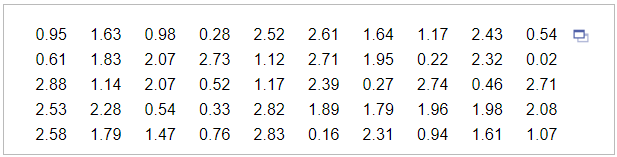
(A.) Find the mean of the data set.
(B.) Determine the median of the data set.
Round to three decimal places as needed.
(C.) Is the magnitude of an earthquake measuring 7.0 on the Richter scale an outlier (data value that is very far away from the others) when considered in the context of the sample data given in this data set? Explain.
I. No, because this value is not the maximum data value.
II. No, because this value is not very far away from all of the other data values.
III. Yes, because this value is very far away from all of the other data values.
IV. Yes, because this value is the maximum data value.
The sample size is a bit large. So, let us: export the data as an Excel file, save it as a Text file (.txt) and import it in RStudio.
(a.) Step 1:
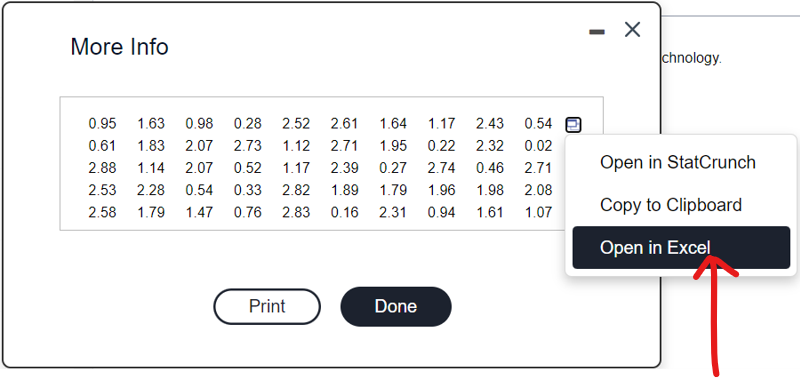
(b.) Step 2:
There is no column name for the data. Let us insert a row and name it:
Data
Then, we can name it with an appropriate name, and save it as a .txt file
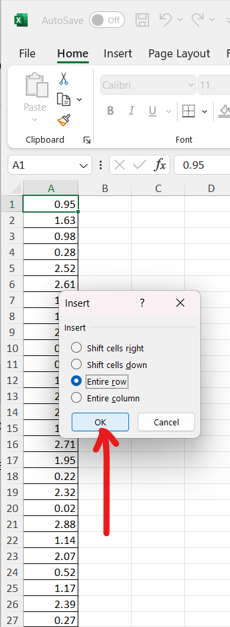
(c.) Step 3:
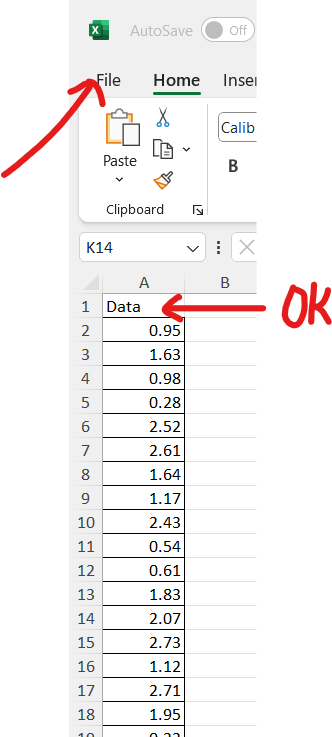
(d.) Step 4:
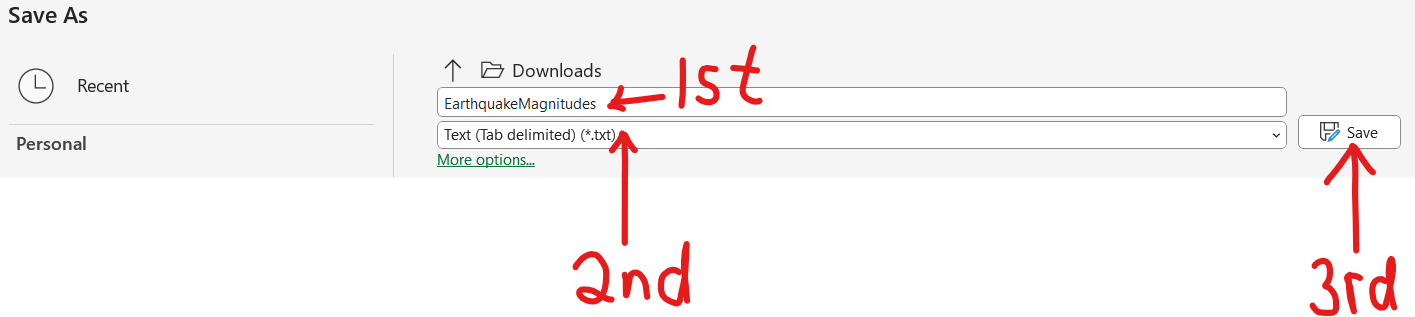
(e.) Step 5:
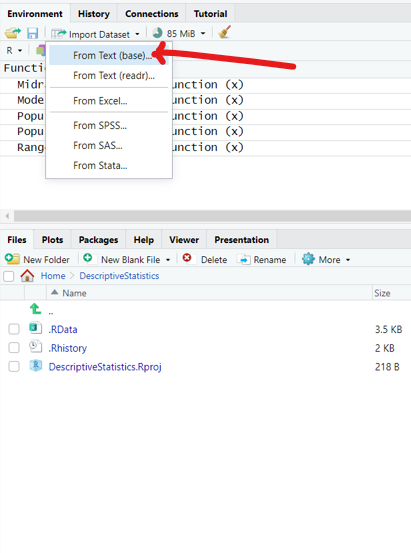
(f.) Step 6:
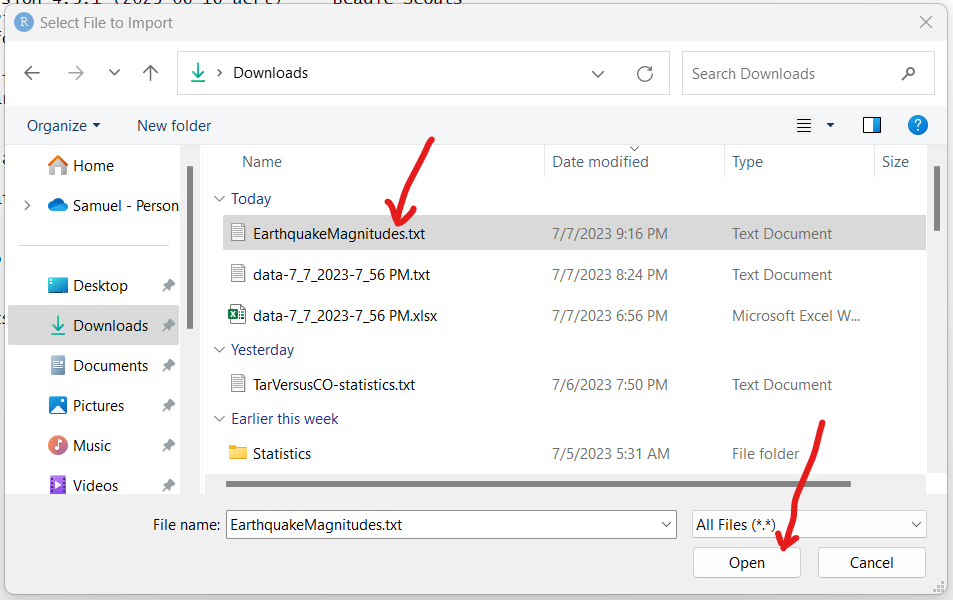
(g.) Step 7:
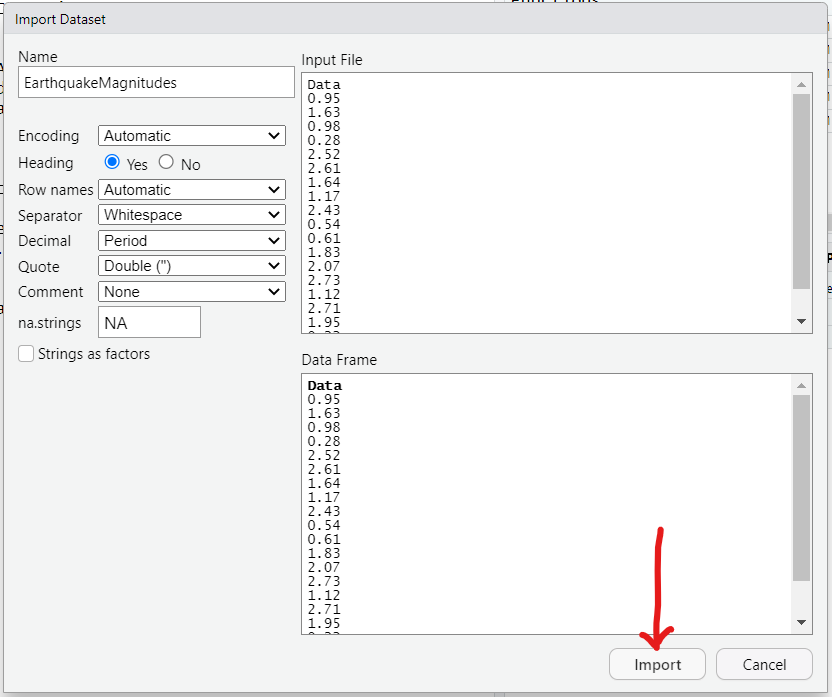
(h.) Questions (A.) and (B.)
We have at least two approaches to solve the question.
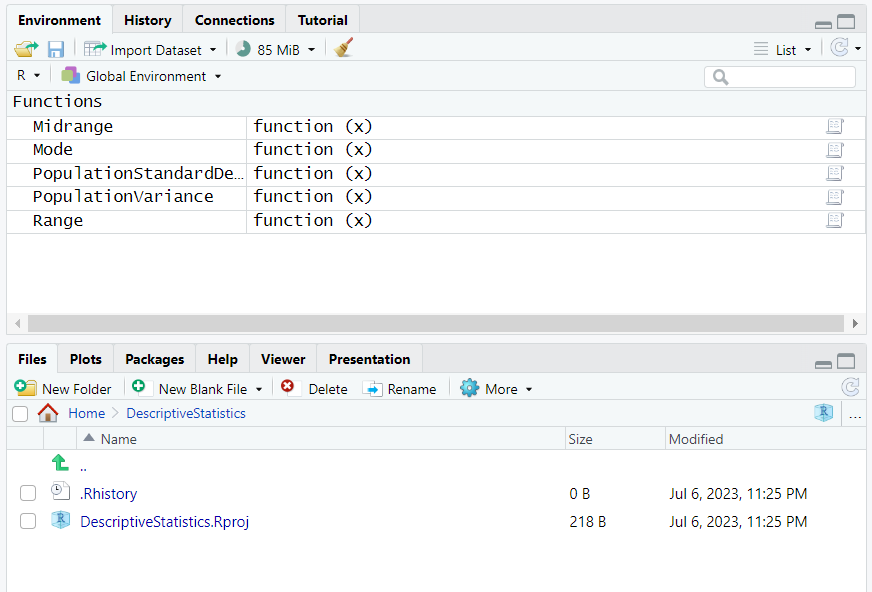
1st Approach: Code Dataset by Column
File Name:
EarthquakeMagnitudes.txt
Column Name:
Data
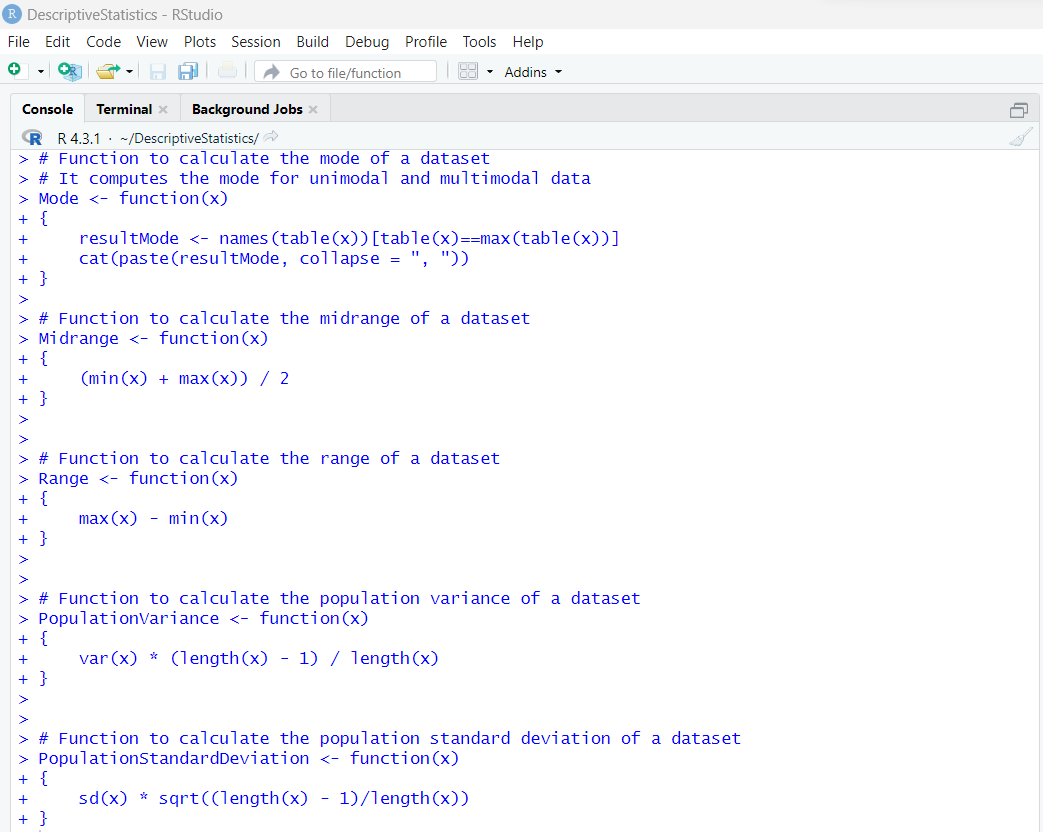
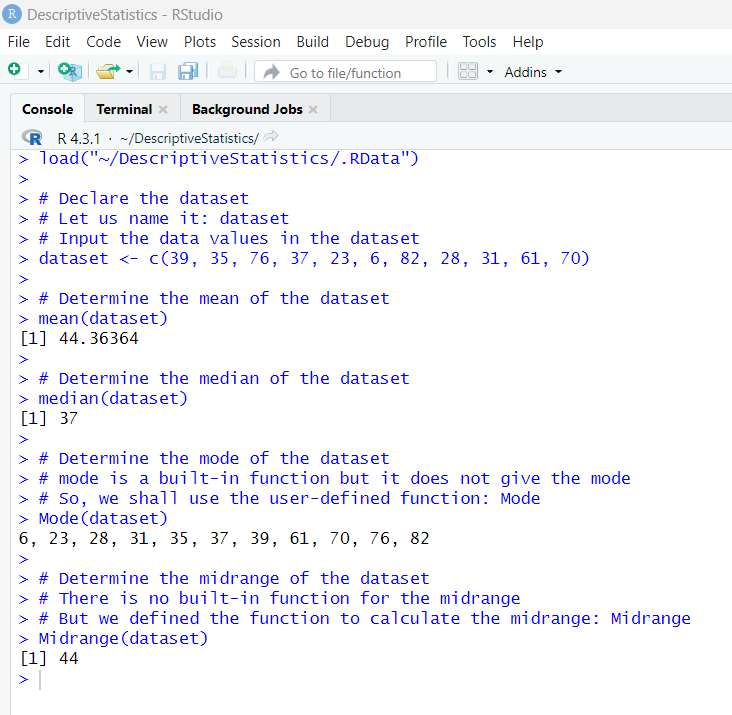
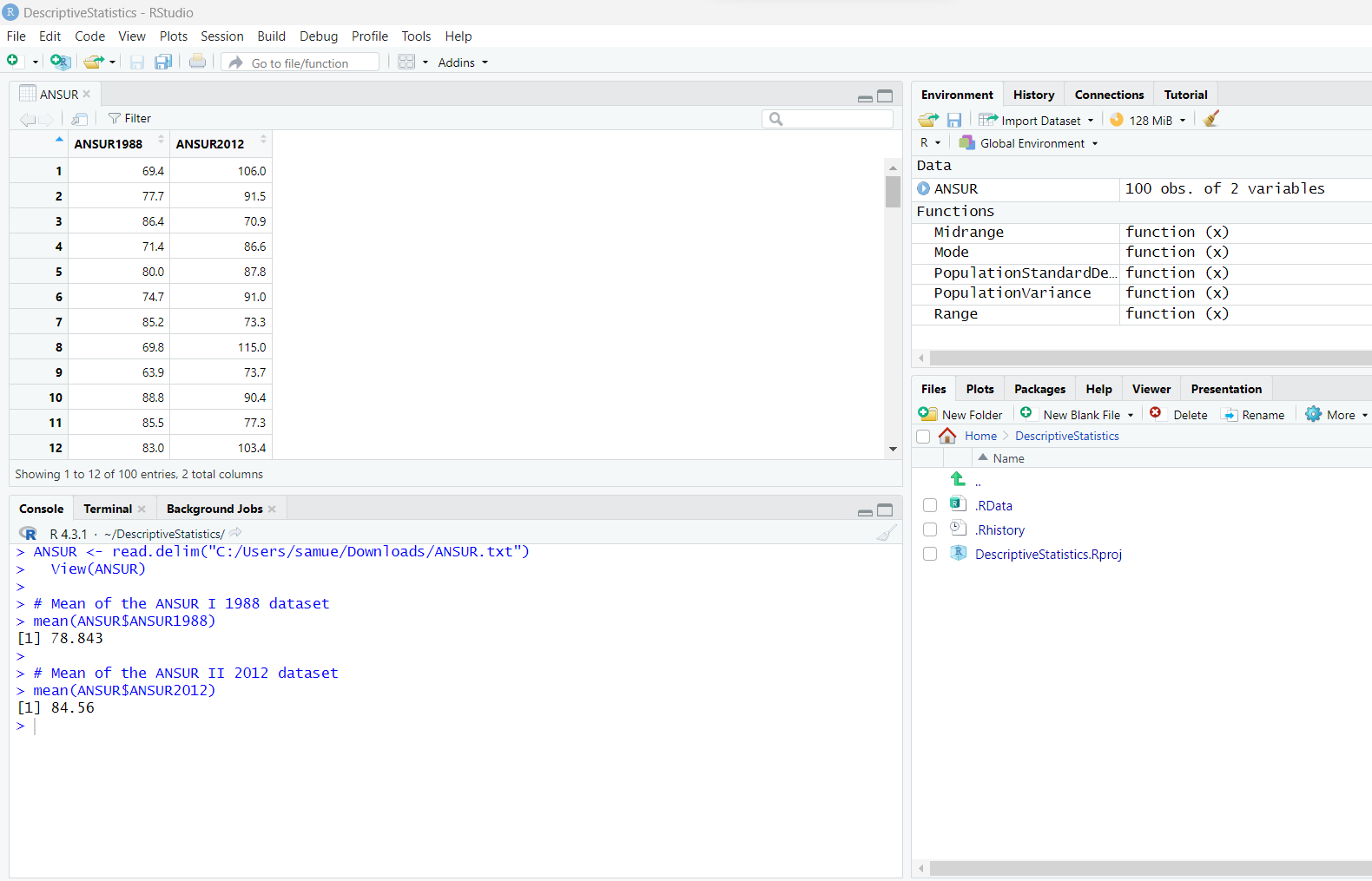
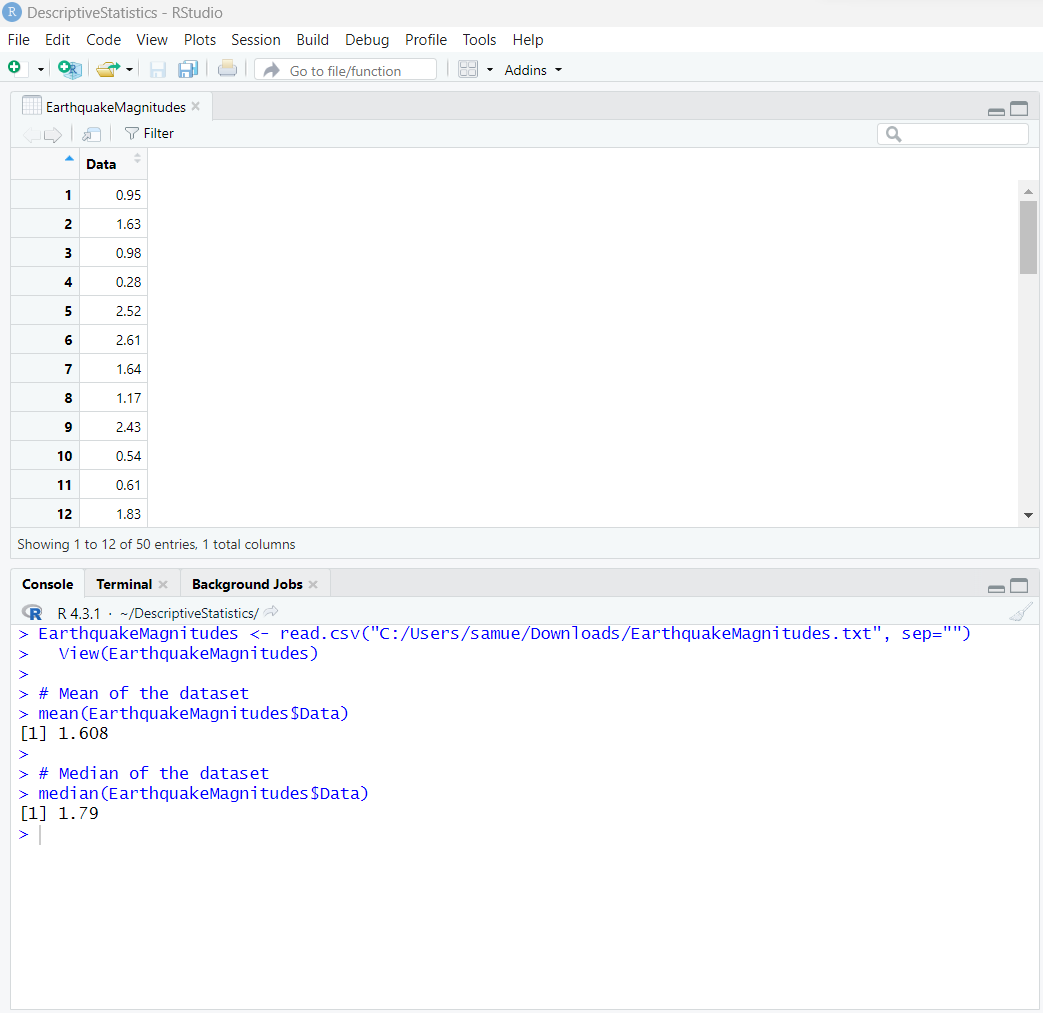
We can go ahead and find the mean and the median.
The code to determine the mean is:
# Mean of the dataset
mean(EarthquakeMagnitudes$Data)
The code to determine the median is:
# Median of the dataset
median(EarthquakeMagnitudes$Data)
 2nd Approach: Code Dataset
2nd Approach: Code Dataset
File Name:
EarthquakeMagnitudes.txt
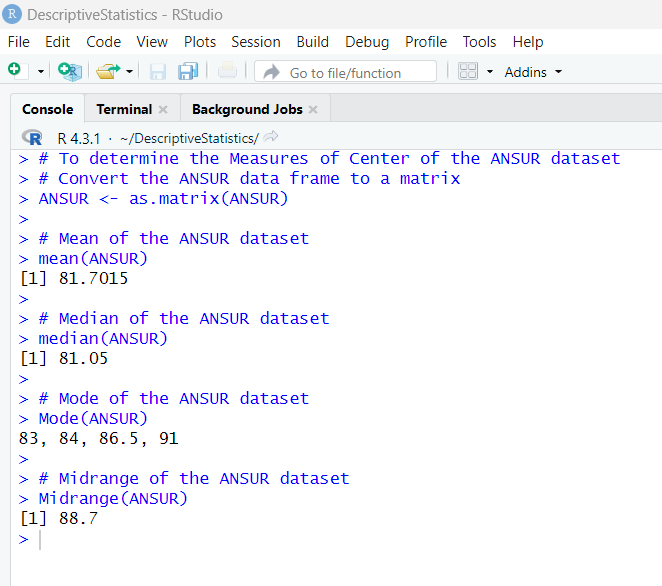
Please see the screenshot below: We need to convert the dataset to a matrix.
The code to convert the dataset to a matrix is:
EarthquakeMagnitudes <– as.matrix(EarthquakeMagnitudes)
Yes, we can use the same file name. I prefer to use the same file name for the converted file (matrix).
However, you may choose a new file name for the matrix.
If I still needed to do more work with the initial file "as is", then I will use a new file name.
The code to determine the mean is:
# Mean of the dataset
mean(EarthquakeMagnitudes)
The code to determine the median is:
# Median of the dataset
median(EarthquakeMagnitudes)
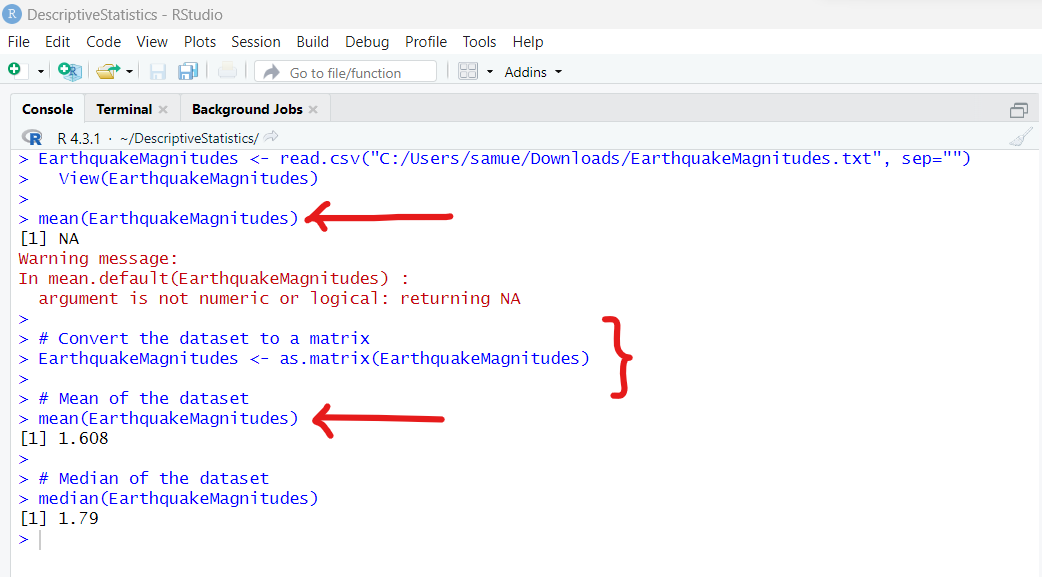
mean = 1.608
median = 1.79
(C.) The dataset: EarthquakeMagnitudes has values from 0.something to 2.something
7.0 is far from these decimals. Hence, it is an outlier when compared to all other data values.
Yes, because this value is very far away from all of the other data values.